ABSORPTION MOLÉCULAIRE

INTRODUCTION
Spectre électromagnétique
Ensemble continu des ondes électromagnétiques connues,
classées dans l'ordre de leurs longueurs d'ondes, de leurs fréquences, de
leurs énergies.
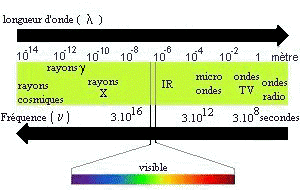
Figure 1 : spectre électromagnétique
Radiations électromagnétiques
La lumière visible est constituée de radiations électromagnétiques
auxquelles l'il humain est sensible.
Ces ondes sont perçues comme étant colorées, tandis que la superposition
de différentes longueurs d'ondes couvrant tout le domaine du spectre visible
constitue une lumière blanche.
Les ondes électromagnétiques sont généralement caractérisées par les
grandeurs suivantes :
longueur d'onde l (lambda) : unité de longueur
(distance) qui sépare deux pics d'onde (exprimé généralement en nm),
nombre d'onde s (sigma) : nombre d'onde par unité
de longueur, (exprimé généralement en cm-1),
fréquence n (nu) : nombre d'onde par seconde
(exprimé en Hz).
Ces grandeurs sont reliées par la relation suivante :
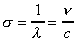 où c la célérité
est la vitesse de la lumière (3.108 m.s-1).
où c la célérité
est la vitesse de la lumière (3.108 m.s-1).
Unités
Selon le domaine considéré, on utilise une unité différente pour la
longueur d'onde par commodité.
En IR
En infrarouge, les longueurs d'onde sont exprimées en
micromètre (µm) appelé aussi micron.
1 µm = 10-6 m = 10-4 cm
Mais pour avoir une grandeur proportionnelle à la fréquence et donc
également proportionnelle à l'énergie on utilise souvent le nombre d'onde
(toujours exprimé en cm-1). Ainsi, à la longueur d'onde de 10µm du
domaine infrarouge correspondent la fréquence 3.1013Hz, le nombre
d'onde s =1000cm-1 et l'énergie 12kJ.mol-1.
En UV / visible
En UV, on utilise essentiellement le nanomètre (nm). 1 nm = 10-9
m

THÉORIE DE LA SPECTROPHOTOMÉTRIE
L'absorption d'un photon correspondant au domaine de longueur
d'onde de l'ultraviolet et du visible, provoque une augmentation de l'énergie
de la molécule de l'ordre de 400000 J.mol-1, conduisant à un
changement de l'état électronique, vibrationnel et rotationnel de la molécule
: h.n = (DE)électronique
+ (DE)vibrationnel + (DE)rotationnel
Équation 1:L'absorption d'un photon se fait par 3 différences
d'énergie
Pour une transition électronique donnée, il existe de nombreuses
possibilités différentes pour des transitions vibrationnelles et
rotationnelles, il y aura donc absorption dans un assez large domaine de
longueur d'onde et si la résolution de l'appareil n'est pas suffisante on
verra, comme c'est souvent le cas, de larges bandes d'absorption ; quelquefois
dans des conditions favorables on pourra résoudre la structure fine de
vibration.
Lorsque le lumière arrive sur un milieu homogène, une partie de cette
lumière incidente est réfléchie, une partie est absorbée par le milieu et le
reste est transmis.
Intensité et flux
L'intensité est un mot qui désigne diverses grandeurs qui n'ont pas la
même dimension. En photométrie, l'intensité est un flux d'énergie par unité
d'angle solide délivré par une source ponctuelle. Or dans la pratique, une
source n'est jamais ponctuelle mais rayonne. L'angle solide est considéré
identique pour la référence et la mesure, on assimile le flux lumineux à
l'intensité.
Si Io est l'intensité de la lumière incidente,
Ir celle de la lumière réfléchie,
Ia celle de la lumière absorbée,
It celle de la lumière transmise, on peut écrire la
relation suivante: Io = Ir + Ia + It
Pierre BOUGUER (1698-1758) en 1729, Jean Henri (Johann Heinrich) LAMBERT
(1728-1777) en 1760 et August BEER (1825-1863) ont particulièrement étudié
les relations qui existent entre l'intensité incidente et l'intensité
transmise. La spectrophotométrie et la colorimétrie sont fondées sur la loi
de Beer - Lambert .
Loi de Bouguer - Lambert
Lorsqu'une lumière monochromatique d'intensité I0
traverse un milieu homogène, l'intensité de la lumière émergente I décroît
exponentiellement lorsque l'épaisseur l du milieu absorbant augmente. 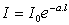
a est une constante appelée coefficient d'absorption,
caractéristique du milieu et de la longueur d'onde considérés.
Loi de Beer
En analyse quantitative, on étudie principalement des
solutions. Dans ce cas, la loi de Beer fait intervenir les concentrations. Elle
s'exprime sous une forme tout à fait semblable à la précédente : 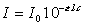
où e est un coefficient d'absorption
caractéristique de la substance appelé coefficient d'extinction, l est
l'épaisseur de la cuve et c la concentration de la solution.
Loi de Beer - Lambert
Finalement la relation fondamentale utilisée en
spectrophotométrie est présentée sous la forme:
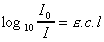 Équation
2 : Loi de Beer - Lambert
Équation
2 : Loi de Beer - Lambert
L'épaisseur de la cuve est exprimée en centimètres, le coefficient
d'extinction dépend de la manière dont est exprimée la concentration de la
solution.
Si la concentration est exprimée en grammes par litre, e est appelé coefficient d'extinction spécifique.
Si la concentration est exprimée en moles par litre, e
est appelé coefficient d'extinction molaire.
Termes à connaître
Certains termes sont d'usage courant en spectrophotométrie.
La densité optique D.O. ou D, encore appelée extinction,
est le logarithme du rapport de l'intensité incidente à l'intensité
transmise. 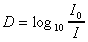
La transmission T est définie comme le rapport de
l'intensité transmise à l'intensité incidente. 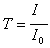
Validité et application de la loi de Beer - Lambert
En général, cette loi est valable dans un large domaine de concentration si
la structure de l'ion, de la molécule ou du composé formé n'est pas modifiée
par une variation de concentration. En général, les écarts à la loi de Beer
- Lambert résultent soit de l'ionisation, soit de la dissociation, soit de
l'association de solutés puisque la nature de l'espèce présente varie en
fonction de la concentration. On observe également des écarts à la loi de
Beer - Lambert lorsque le soluté forme des complexes, la composition de ces
derniers dépendant de la concentration, ou lorsqu'il s'agit de solutions
fluorescentes ou de suspensions.
Enfin, pour que la loi de Beer - Lambert soit
vérifiée, il faut utiliser une lumière monochromatique.
Voir aussi :


![]()